AntCTF & Dˆ3CTF 2022（d3arm+d3w0w）

d3arm

得到了一个bin的文件，如果想要得到代码需要将这个bin文件转化成hex文件，使用bintohex这个软件，得到hex文件，然后将这个hex文件载入到ida之中，将hex文件载入ida的时候需要设置一些参数，这个过程可以参考这篇文章

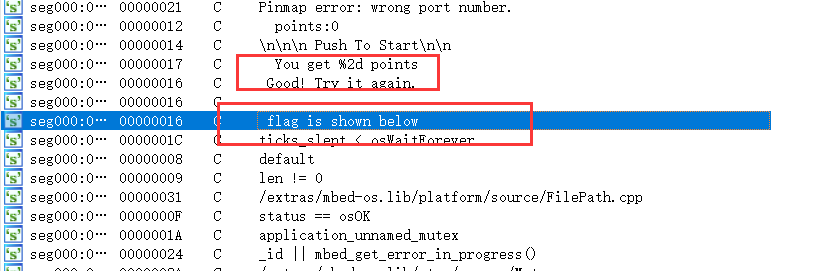
将这个hex文件载入ida之中之后，查看字符串，根据图中标记的字符串跟进到关键代码的位置

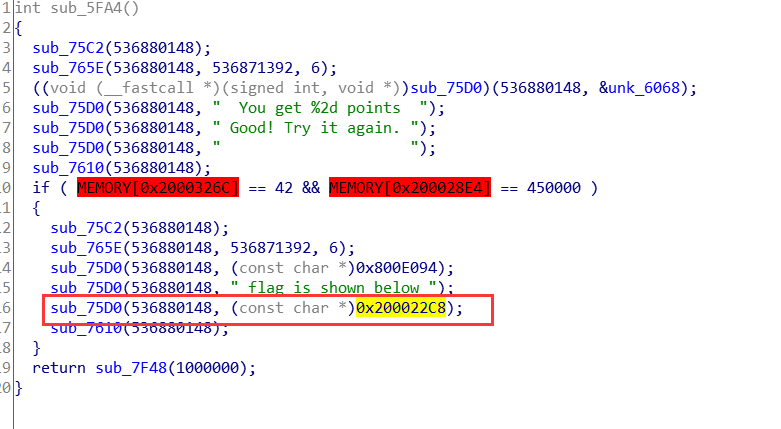
关键主代码

图中标记的地方就是可能是flag的地方

引用了flag的函数

在这个函数里面不能够得到什么数值的有效信息，所以查看引用该函数的其它函数，但是这里通过交叉函数我并不能找到有效的函数，翻看这个函数上下的函数，找到一个引用了point和flag地址的一个函数，将point作为下标，给flag进行赋值的操作

通过地址0x800DB64，在汇编代码的界面之宗，点击G 输入跳转到0x000DB64这个地址，就可以找到这个数组了

这个数组是（上图之中只是部分的数据，一共要取42个数字）

[0x20,0x6d,0x50,0x30,0x38,0x48,0x20,0x6d,0x5,0x26,0x6d,0x56,0x72,0x6d,0x51,0x22,0x6c,0x4,0x70,0x38,0x0,0x26,0x6a,0x57,0x27,0x6a,0x57,0x74,0x6b,0xa,0x27,0x38,0x1,0x75,0x6a,0x5,0x27,0x68,0x3,0x26,0x3a,0x4e]

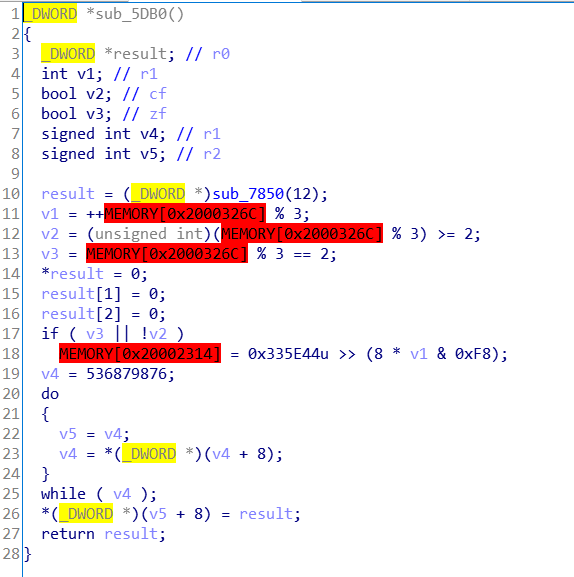
异或的对象MEMORY[0x20002314]

但是现在还不知道这个数组异或的对象MEMORY[0x20002314]的内容

找到和这个地址的数相关的函数，这个函数有对这个地址赋值的操作，其中的MEMORY[0x20002314] = 0x335E44u >> (8 * v1 & 0xF8)这个式子中的v1来自于 MEMORY[0x2000326C] % 3，MEMORY[0x2000326C]和上一个函数相得知是数组的下标，异或的对象有3种0x44、0x5E、0x33,根据MEMORY[0x2000326C] % 3的结果作为下标来决定异或的对象

脚本：

obj = [0x20,0x6d,0x50,0x30,0x38,0x48,0x20,0x6d,0x5,0x26,0x6d,0x56,0x72,0x6d,0x51,0x22,0x6c,0x4,0x70,0x38,0x0,0x26,0x6a,0x57,0x27,0x6a,0x57,0x74,0x6b,0xa,0x27,0x38,0x1,0x75,0x6a,0x5,0x27,0x68,0x3,0x26,0x3a,0x4e]
key = 0x335E44
for i in range(len(obj)):
  temkey = (key>>((i%3)*8)) & 0xff
  print(chr(temkey^obj[i]),end='')
d3ctf{d36b3e63bf274f3b4dc4d059cf2146c60bd}

d3ctf{d36b3e63bf274f3b4dc4d059cf2146c60bd}

d3w0w

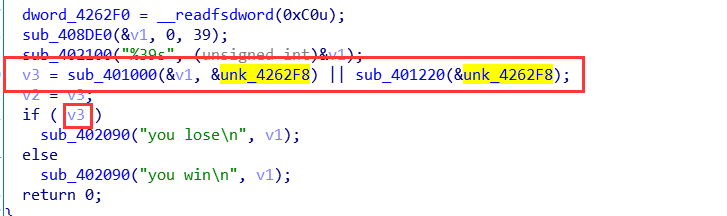
使用32位的ida打开这个程序，通过程序之中的字符串定位到关键的代码

分析代码显然我们需要使得这两个函数都能够返回0，这里我们得到的v3的结果就是0

第一个函数 sub_401000(&v1, &unk_4262F8)

第一个函数 sub_401000(&v1, &unk_4262F8) 其中的v1代表我们输入的flag的值，这个flag里面有四种char 1，2，3，4，利用这个flag的字符串用走迷宫的形式给这个数组赋值

32位程序调用64位函数：

rewolf-wow64ext的目的就是让运行在Wow64环境中的x86应用程序可以直接调用x64下ntdll.dll中的Native API。

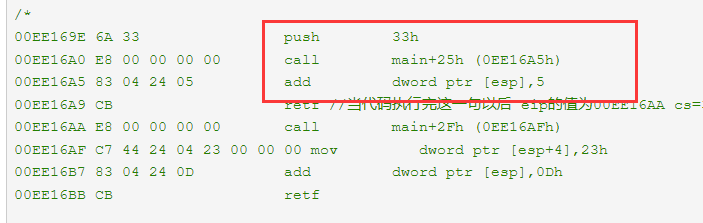
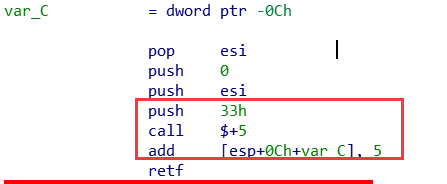
进程的32位模式改为64位模式的具体代码：

主要方法是借助retf将CS寄存器的值设置为0x33。

为什么要将CS寄存器的值设置为0x33？因为我们所需CPU的解码模式需要是64位模式，而当前模式是32位。64位CPU是通过GDT表中CS段所对应的表项中L标志位来确定当前解码模式的。

在x64系统下的进程是有32位和64位两种工作模式，这两种工作模式的区别在于CS寄存器。32位模式时，CS = 0x23；64位模式时，CS = 0x33。

切换这两种工作模式的方法：

一般会通过retf指令，retf指令和 pop ip+pop cs 作用相同。如果此时栈中有0x33，则会将0x33弹出到CS寄存器中，实现32位程序切换到64位代码的过程

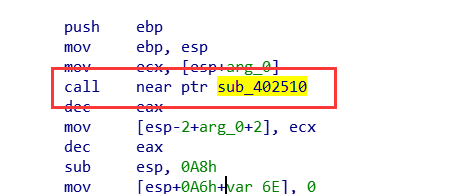
我们直接打开这个函数，不能够反编译，然后现在查看汇编代码，在程序的开头就调用了一个函数

跟进到这个函数之中去，发现了和32需要调用64位函数的时候的中间代码相同的一段代码，这样我们就能知道这个地方的函数是64位的

第二个函数 sub_401220(&unk_4262F8)

这个函数的参数就是在上一个函数赋值的数组，这个函数里面就是对这个赋值得到的数组进行一系列的限制，但是这个地方是一个32位的程序之中调用64位的函数，所以我们需要将这个函数dump出来，然后导入到ida64之中去反编译这个函数，但是这里的代码之中即有32位的代码又有64位的代码，这样做是不能通过这样的方法反编译出来的。

但是使用ida7.5反编译这个程序就能够得到这个函数的代码，但是这个代码之中会混杂着一些asm的汇编代码，需要我们仔细地分析这个代码。

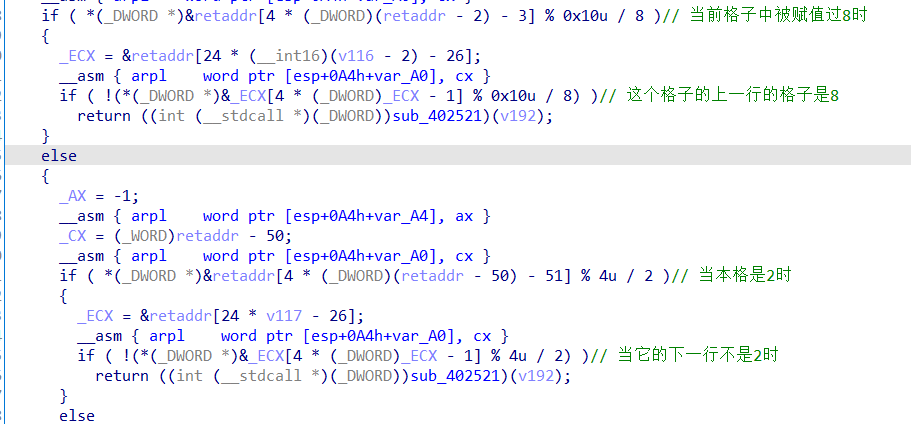
这里面参杂着一些64位的汇编代码，它的代码意义在图中有标明进行注释

对迷宫的第一排第一列第六排第六列的限制

第一种特殊点的限制

限制1 ：不能同时含有 8 和 2 并且也不能同时含有4和1 所以有12、9、6、3这四种组合方式

限制2 ：需要赋值两次

限制三：

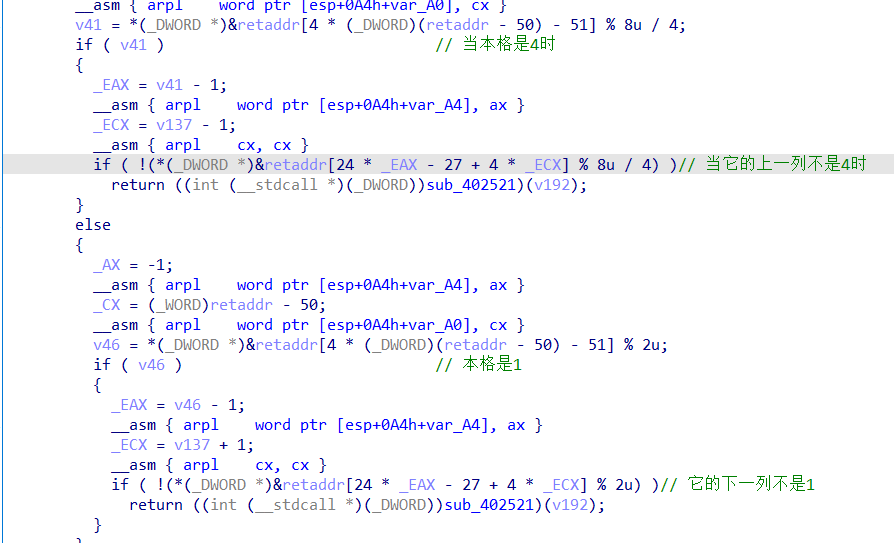
如果当前的格子之中是8 则它的上一行的对应的格子就不能是8

如果当前的格子之中是2 则它的下一行的对应的格子就不能是2

如果当前的格子之中是4 则它的上一格的对应的格子就不能是4

如果当前的格子之中是1 则它的上一行的对应的格子就不能是1

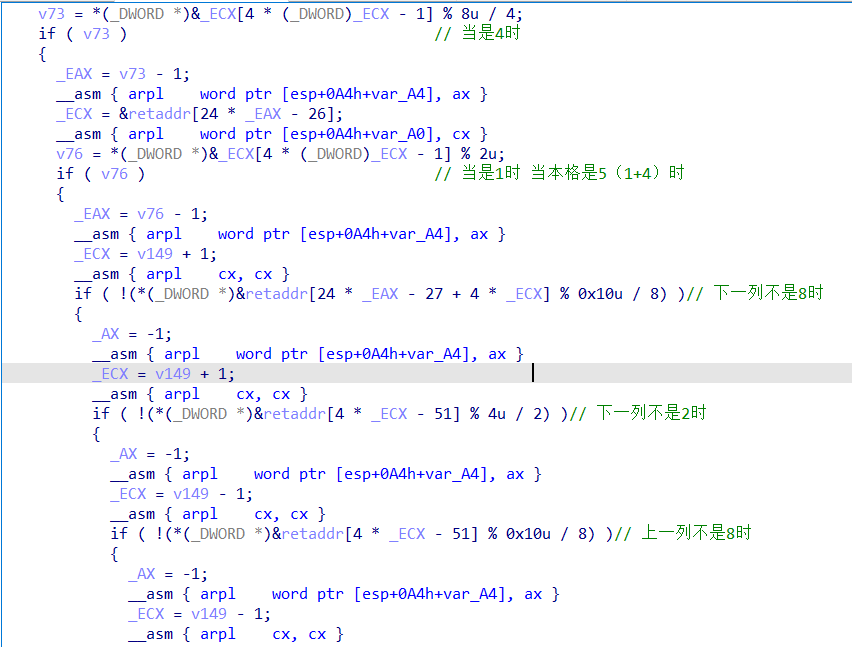
第二种特殊点的限制

限制一：这十个坐标含有2和8的组合或者含有1和4的组合

限制二：

当本格是10时，上下两行之中一定要含有1或4

当本格是5时，左右两格之中一定要含有8或2

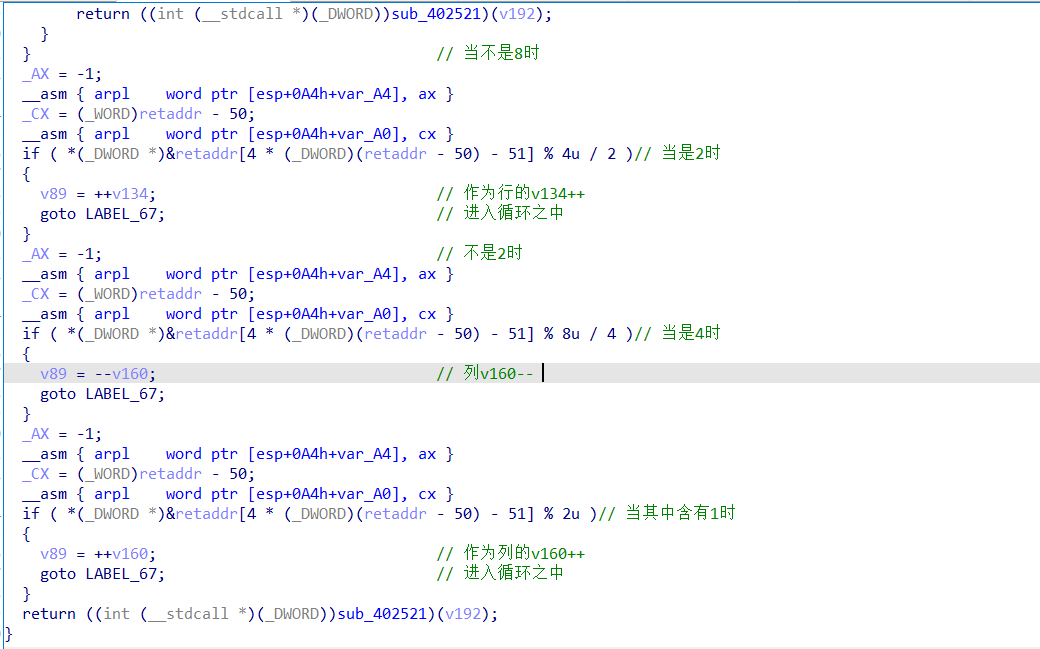
对走的方向以及迷宫终点设置的代码

整理之后地代码

别人的wp之中找到对这部分代码的整理之后的结果：

spoint1[0] = 0;
  spoint1[1] = 14;
  spoint1[2] = 20;
//总体限制，不能撞墙，不能重复使用格子
  for ( i = 0; i < 6; ++i )
  {
    for ( j = 0; j < 6; ++j )
    {
      if ( table[6 * i + j] > 0xFu )            // 每一个格子都不能大于16
        return 1i64;
      v14 = table[6 * i + j] % 0x10u / 8;
      v22 = j;
      v15 = table[6 * i + j] % 8u / 4 + v14;
      v23 = j;
      v16 = table[6 * i + j] % 4u / 2 + v15;
      v24 = j;
      if ( table[6 * i + j] % 2u + v16 > 2 )    // 计算二进制1的个数,也就是说每个格子不能被设置两次以上
        return 1i64;
      if ( !j && table[6 * i] % 8u / 4 )        // 6*6数组的第一列不能=4
        return 1i64;
      if ( j == 5 && table[6 * i + 5] % 2u )    // 最后一列不能=1
        return 1i64;
      if ( !i && table[j] % 0x10u / 8 )         // 第一行每一个都不能=8
        return 1i64;
      if ( i == 5 && table[j + 30] % 4u / 2 )   // 最后一行每一个都不能=2
        return 1i64;
    }
  }
  //第一种特殊点限制条件，这种特殊点周围不能连着出现两种操作，碰到必须拐弯
  for ( k = 0; (unsigned __int64)k < 3; ++k )
  {
    row1 = spoint1[k] / 10;                     // 0 1 2
    col1 = spoint1[k] % 10;                     // 0 4 0
    if ( table[6 * row1 + col1] % 0x10u / 8 && table[6 * row1 + col1] % 4u / 2 )// != 8 != 2
      return 1i64;
    if ( table[6 * row1 + col1] % 8u / 4 && table[6 * row1 + col1] % 2u )// != 4 != 1
      return 1i64;
    v17 = table[6 * row1 + col1] % 0x10u / 8;
    v25 = col1;
    v18 = table[6 * row1 + col1] % 4u / 2 + v17;
    v26 = col1;
    v19 = table[6 * row1 + col1] % 2u + v18;
    v27 = col1;
    if ( table[6 * row1 + col1] % 8u / 4 + v19 != 2 )
      return 1i64;
    if ( table[6 * row1 + col1] % 0x10u / 8 )   // 当前格子为8则判断上一行不能为8
    {
      if ( !(table[6 * row1 - 6 + col1] % 0x10u / 8) )
        return 1i64;
    }
    else if ( table[6 * row1 + col1] % 4u / 2 ) // 当前格子为2则判断下一行不能为2
    {
      if ( !(table[6 * row1 + 6 + col1] % 4u / 2) )
        return 1i64;
    }
    else if ( table[6 * row1 + col1] % 8u / 4 ) // 当前格子为4则判断上一格不能为4
    {
      if ( !(table[6 * row1 - 1 + col1] % 8u / 4) )
        return 1i64;
    }
    else if ( table[6 * row1 + col1] % 2u && !(table[6 * row1 + 1 + col1] % 2u) )// 当前格子为1则判断下一格不能为1
    {
      return 1i64;
    }
  }
  //第二种特殊点限制条件，必须直线进入，连续3格可连成直线，并且是拐弯进入前一格，或者进入后一格后拐弯
  spoint2[0] = 4;
  spoint2[1] = 13;
  spoint2[2] = 15;
  spoint2[3] = 21;
  spoint2[4] = 24;
  spoint2[5] = 31;
  spoint2[6] = 32;
  spoint2[7] = 41;
  spoint2[8] = 45;
  spoint2[9] = 53;
  for ( l = 0; (unsigned __int64)l < 0xA; ++l )
  {
    row2 = spoint2[l] / 10;
    col2 = spoint2[l] % 10;
    if ( (!(table[6 * row2 + col2] % 0x10u / 8) || !(table[6 * row2 + col2] % 4u / 2))// 只有 28 或者14的组合
      && (!(table[6 * row2 + col2] % 8u / 4) || !(table[6 * row2 + col2] % 2u)) )
    {
      return 1i64;
    }
    if ( table[6 * row2 + col2] % 0x10u / 8     // 28组合
                                                // 上一行 =4 =1或者
                                                // 下一行 =4 =1
      && table[6 * row2 + col2] % 4u / 2
      && !(table[6 * row2 - 6 + col2] % 8u / 4)
      && !(table[6 * row2 - 6 + col2] % 2u)
      && !(table[6 * row2 + 6 + col2] % 8u / 4)
      && !(table[6 * row2 + 6 + col2] % 2u) )
    {
      return 1i64;
    }
    if ( table[6 * row2 + col2] % 8u / 4        // 14组合
                                                // 上一格 =2 =8或者
                                                // 下一格 =2 =8
      && table[6 * row2 + col2] % 2u
      && !(table[6 * row2 + 1 + col2] % 0x10u / 8)
      && !(table[6 * row2 + 1 + col2] % 4u / 2)
      && !(table[6 * row2 - 1 + col2] % 0x10u / 8)
      && !(table[6 * row2 - 1 + col2] % 4u / 2) )
    {
      return 1i64;
    }
  }
  //校验,使用数组的值移动点，最后能回到(0,0)点就是flag了
    oldrow = 0;
  v11 = 0;
  row3 = 0;
  col3 = 0;
  if ( *table % 0x10u / 8 )
  {
    row3 = -1;                                  // 前一行
    do
    {
LABEL_79:
      if ( !(table[6 * row3 + col3] % 0x10u / 8) || row3 - 1 == oldrow && col3 == v11 )// 8则转到上一行
      {
        if ( !(table[6 * row3 + col3] % 4u / 2) || row3 + 1 == oldrow && col3 == v11 )// 2
        {
          if ( !(table[6 * row3 + col3] % 8u / 4) || row3 == oldrow && col3 - 1 == v11 )// 4
          {
            if ( !(table[6 * row3 + col3] % 2u) || row3 == oldrow && col3 + 1 == v11 )// 1
              return 1i64;
            oldrow = row3;
            v11 = col3++;
          }
          else
          {
            oldrow = row3;
            v11 = col3--;
          }
        }
        else
        {
          oldrow = row3;
          v11 = col3;
          ++row3;
        }
      }
      else
      {
        oldrow = row3;
        v11 = col3;
        --row3;
      }
    }
    while ( row3 || col3 );
    result = 0i64;
  }
  else
  {
    if ( *table % 4u / 2 )
    {
      row3 = 1;                                 // 后一行
      goto LABEL_79;
    }
    if ( *table % 8u / 4 )
    {
      col3 = -1;                                // 前一格
      goto LABEL_79;
    }
    if ( *table % 2u )
    {
      col3 = 1;                                 // 后一格
      goto LABEL_79;
    }
    result = 1i64;
  }
  return result;

总结第二个函数中对迷宫的限制

通过第一个函数我们可以知道每当一个格子被设置值（方向）的时候，它所到达的下一个格子也会被设置一个值（方向），下一个格子的值（方向）是和当前格子相反的方向，也就是下一个格子含有指向当前格子的方向，所以迷宫走的路径是双向设置的（每一步都是双向的），既能够正着走，也能够反着走，在特殊点的性质设置的时候也会利用到这个迷宫设置的这个特点。
这个迷宫中的数据都要被设置两次
迷宫的第一列不能是4

迷宫的第六列不能是1

迷宫的第一排不能是8

迷宫的第六排不能是2

对坐标为（0,0）（1,4）（2,0）的限制（坐标的第一个是行第二个是列）

这个单元格中不能同时含有 8 和 2 并且也不能同时含有4和1
需要被赋值两次（采用和开头相同的检验是否被赋值了两次以上的检验方法）
如果当前的格子之中是8 则它的上一行的对应的格子就不能是8
如果当前的格子之中是2 则它的下一行的对应的格子就不能是2
如果当前的格子之中是4 则它的上一格的对应的格子就不能是4
如果当前的格子之中是1 则它的上一行的对应的格子就不能是1
这种特殊点周围不能连着出现两种操作，碰到必须拐弯。
- 它自身就必须含有水平和竖直方向的移动各一种
- 这种特殊节点需要连接两个格子（通过自己有的两个方向能够到达这两个格子），所以这两个格子需要分别存在于它的水平和竖直方向上，那么在这个节点必定要转弯

对坐标(0,4) (1,3) (1,5) (2,1) (2,4) (3,1) (3,2) (4,1) (4,5) (5,3)的限制

这十个坐标含有2和8的组合或者含有1和4的组合（因为在程序的最开始就标注了每个格子被设置的次数不能超过2次，所以这10个坐标的设置只能是这两种组合种的一种，也就是这10个格子的数值只能是10或者5）
当本格是10时，上下两行之中一定要含有1或4（在本格之中即能向上走也能向下走）
当本格是5时，左右两格之中一定要含有8或2（在本格之中既能向左走也能向右走）
第二种特殊点限制条件，必须直线进入，连续3格可连成直线，并且是拐弯进入前一格，或者进入后一格后拐弯。
- 这种特殊点需要能够到达它的前后两个节点（连接两个格子），但是它自己本身这个格子之中方向的定义只有一种类型（竖直方向的或者水平方向的）。所以它的前后两个格子和它自身必须在同一条直线上，那么这样就使得进入这个格子的方向，就是这个格子所具有的方向（水平还是竖直）。
- 因为第二三个条件的限制使得，它连接的两个格子之中会有转弯的方向，如果是它的前一个格子含有转弯的方向，说明是拐弯进入前一格的。如果它的后一个格子含有转弯的方向，说明进入后一格后拐弯。

走迷宫的规则和操作：

8是向上走 2是向下走 4是向左走 1是向右走（判断的顺序是8 2 4 1）
不能再回到上一格的位置
走到终点的位置是（0，0）

走迷宫

使用#标注第一种类型的特殊点使用$来标注第二种特殊类型的点从上一个函数我们可以知道第一个位置固定是

  0  1  2  3  4  5 
0 #3 05 05 05 $5 06  
1 0A 0  03 $5 #4 $A
2 #9 $5 0C 0  $A 0A
3 03 $5 $5 06 0A 0A
4 09 $5 06 09 0C $A
5 0  0  09 $5 05 0C

[3, 5, 5, 5, 5, 6] 
[A, 0, 3, 5, 6, A] 
[9, 5, C, 0, A, A] 
[3, 5, 5, 6, A, A] 
[9, 5, 6, 9, C, A] 
[0, 0, 9, 5, 5, C]

idx	1	2	3	4	5	6
1	#↓	←	←	←	*←	←
2	↓	0	→	*→	#↓	*↑
3	#→	*→	↑	0	*↓	↑
4	↓	*←	*←	←	↓	↑
5	→	*→	↓	↑	←	*↑
6	0	0	→	*→	→	↑

上面这个是走迷宫的过程，得到的按着这个方向正着走到最后之后再按着同样的路线反着走一次就能够得到这个目标的6*6的map了

按照第一个函数的赋值的方式就能够得到这个过程是 d3ctf{22441442223133324424441111133333}

所以最后得到的flag是 d3ctf{22441442223133324424441111133333}